前回に引き続き、今回もグラフ機械学習についてです。
教科書はこちらです。
今回は特に、グラフにおける表現学習について紹介します。
一般に表現学習とは、(機械学習を用いた)予測器を構築する際に有用な情報を抽出しやすくするためのデータの表現を学習することです。[1]Bengio大先生の論文"Representation learning: A review and new perspectives"では、> representation learning, i.e., learning representations of the data that make it easier to extract useful information when building classifiers or other predictors. と述べられています。
グラフの表現学習
グラフ機械学習では、グラフという(画像や音声データと比較して)複雑な構造に対して検知や潜在パターンの解釈を行います。
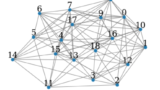
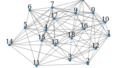
その前段の処理として、グラフを数値化(ベクトル化)したいわけですが、下図のようにどのインスタンス(ノード、エッジ、グラフ自体)を対象としたいかによって、ベクトル化には様々なパターンが存在します。
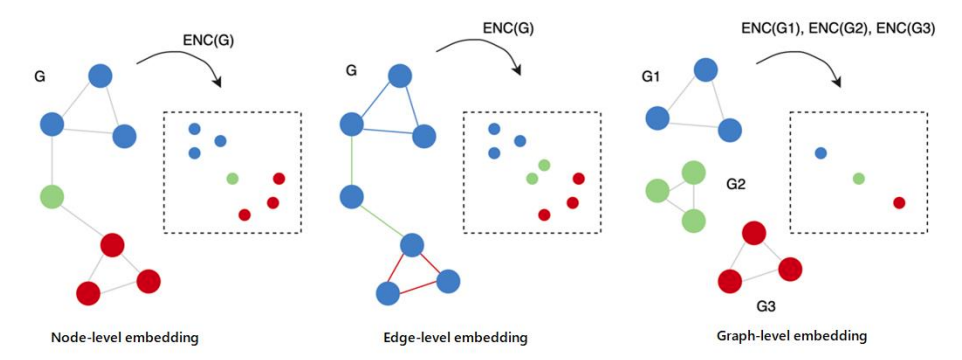
グラフ機械学習の文脈では、このように与えられたインスタンスの適切な特徴表現を学習(正確には、与えられたインスタンスを適切な特徴ベクトルに写像する関数の学習)する手続きをrepresentation learning(表現学習)や(network)embedding((ネットワーク)埋め込み)[2]この手続によって得られた特徴ベクトルをembeddingと呼んだりもします。と呼んでいます。
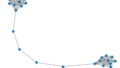
この手続きを図にすると、以下のようになります。
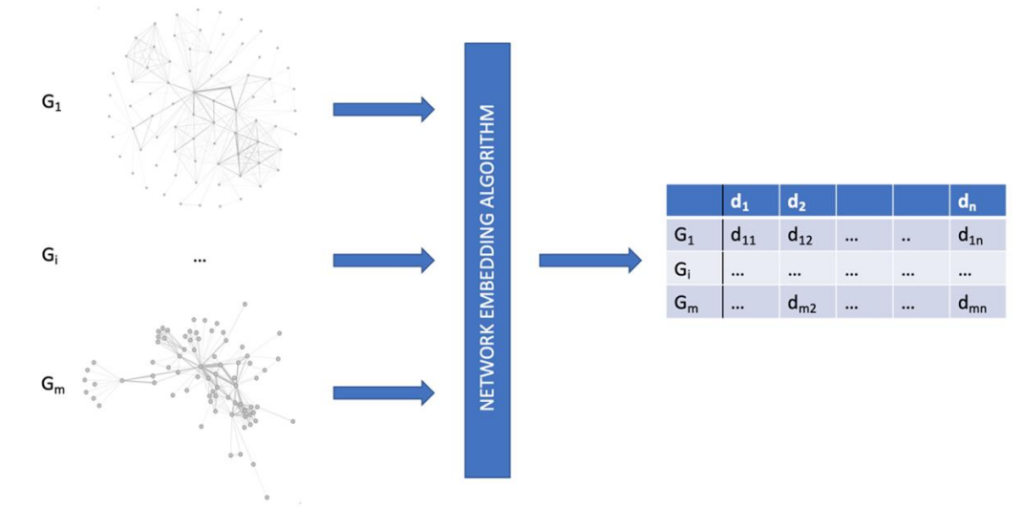
グラフがベクトル化されているのが分かりますね。
embeddingのためのアルゴリズムは4つのカテゴリに大別できます。[3]書籍では以下のようにカテゴリが大別されてますが、この章は説明が非常に少なく、今の段階ではよく分からなくて普通です。
- Shallow embedding: 入力インスタンスに対して、行列分解やWord2vec的なことをやる手法。学習したデータのembedding(ベクトル表現)のみをそのまま返す。[4]この手法のみ、学習した関数を使って未知のインスタンスに対する埋め込みベクトルを生成することができない。
- Graph autoencoding: 単に入力インスタンスをベクトル表現に変換するのではなく、より一般的な写像関数を学習する手法。
- Neighborhood aggregation: グラフの内部構造だけでなく、そのノードに付与される属性情報も考慮した埋め込み空間を構築できる手法。[5]例えば、構造が似ていてノードの性質が異なるグラフを識別することができる埋め込み空間を持つことができる。
- Graph regularization: 上記3つと異なり、グラフ正則化に基づく手法は入力としてグラフを持たなず、その代わりに正則化するために特徴の相互作用を利用し、特徴の集合から表現を学習する手法。[6]よく分からない説明になってしまっていますが、詳細は4章で説明されます。4章の説明を読んでもあまりよく分かりませんでしたが…。
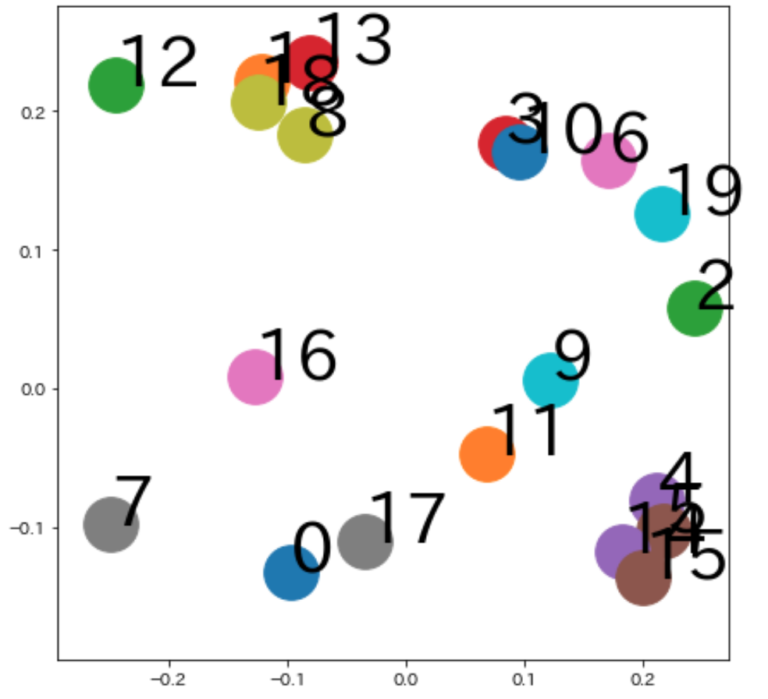
こちらのノートブック内で、shallow embeddingの例(Node2vec, Edge2vec, Graph2vec)をPythonコードと共に紹介しています。
表現学習で使われる損失関数
(以下はややこしめの話なので、とりあえず無視して大丈夫です。)
グラフ表現学習では、以下のような2項の損失関数が一般的に使われます。
$$Loss = \alpha L_{sup}(y, \hat{y}) + L_{rec}(G, \hat{G})$$
$L_{sup}$: 実際のクラス$y$と予測されたクラス$\hat{y}$のエラーを表す(教師無しだと$\alpha=0$)
$L_{rec}$: 入力グラフ$G$とエンコーダ・デコーダで得られた$\hat{G}$のエラーを表す
単純なクラス予測のエラーだけではなくて、入力グラフとそれを圧縮して復元した結果のグラフのエラーも考慮されていて、グラフの表現学習に使えそうな雰囲気が漂ってますね。
今回の説明は以上になります。お疲れ様でした。
より詳しい説明はこちらの本をご参照ください。
注釈
| ↩1 | Bengio大先生の論文"Representation learning: A review and new perspectives"では、> representation learning, i.e., learning representations of the data that make it easier to extract useful information when building classifiers or other predictors. と述べられています。 |
|---|---|
| ↩2 | この手続によって得られた特徴ベクトルをembeddingと呼んだりもします。 |
| ↩3 | 書籍では以下のようにカテゴリが大別されてますが、この章は説明が非常に少なく、今の段階ではよく分からなくて普通です。 |
| ↩4 | この手法のみ、学習した関数を使って未知のインスタンスに対する埋め込みベクトルを生成することができない。 |
| ↩5 | 例えば、構造が似ていてノードの性質が異なるグラフを識別することができる埋め込み空間を持つことができる。 |
| ↩6 | よく分からない説明になってしまっていますが、詳細は4章で説明されます。4章の説明を読んでもあまりよく分かりませんでしたが…。 |

コメント