今回はグラフに対する教師無し学習を紹介します。
特にグラフニューラルネットワークで有名なGraph Convolutional Networks(GCN)を取り上げ、Python(numpy)で実装します。
教科書はいつものこちらです。
教師無し学習
教示無し学習は機械学習の一種で、データの背後にある構造を捉えるのに適しており、クラスタリングや次元削減に用いられます。[1]グラフ機械学習では、ノード分類などの下流タスクの前段として重宝されます。
グラフに対する教師無し学習(特にグラフの表現学習)の分類は以下のとおりです。
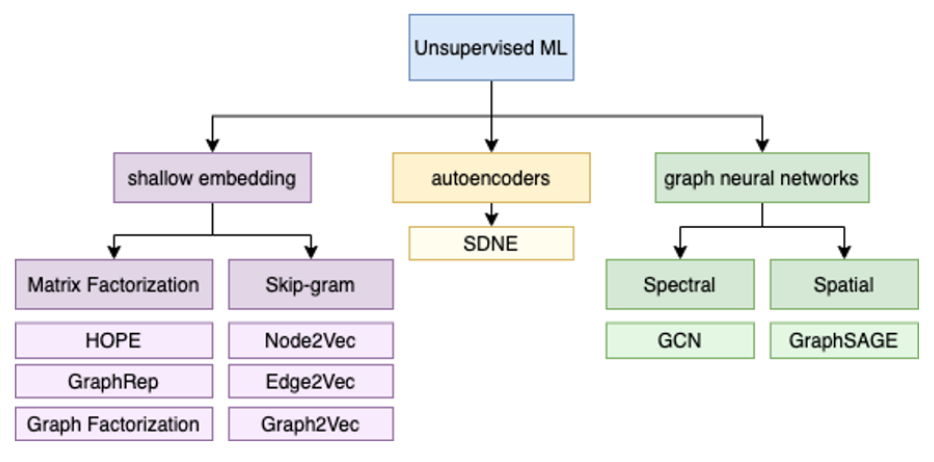
Shallow embedding系:
・Matrix Factorization系: 入力グラフの隣接行列を行列分解する手法[2]行列分解の解説はこちらの記事が分かりやすいです。[3]最適化時の損失関数の工夫で、得られるembeddingの特徴を変えられる。。
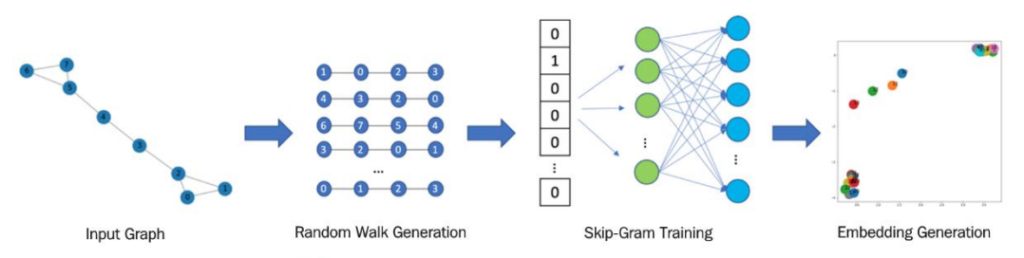
・Skip-gram系: 自然言語処理でお馴染みのWord2vecでも使われているSkip-gram。グラフの繋がっているノードの一部を並べた列をWord2vecでいうところの単語列とみなして、ニューラルネットに入力して分散表現を得る。embeddingの流れは以下のとおりです。
Autoencoder系: 次元圧縮でお馴染みのオートエンコーダ・デコーダを活用したもの。詳しい説明はこちら[4]非線形な活性化関数を用いると、非線形な変換ができる。巨大なグラフには適さない。。
Graph neural networks (GNN)系: グラフ構造データに対して(ディープ)ニューラルネットワークを適用する手法[5]グラフデータを扱うニューラルネットワークについては、こちらのサーベイ発表が面白いです。。
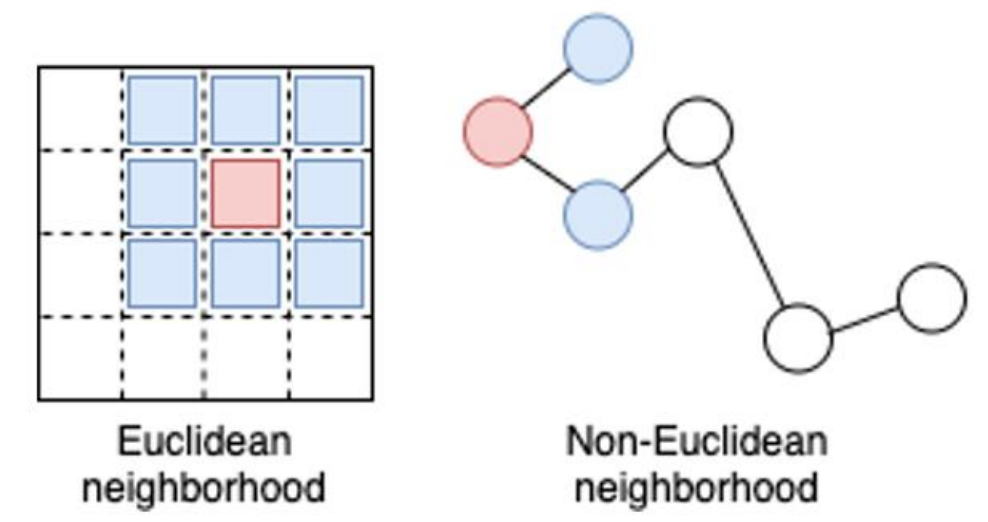
グラフデータは下図のように非ユークリッド空間に定義されるので、例えばCNNのような畳み込みフィルタを直接適用するわけにはいかず、グラフ特有の工夫が必要です。
GNNは、2009年にScarselli et al. によって提案されました。 この手法は、各ノードの特徴を自身とその近傍の特徴によって表せるという前提に基づき、最近傍ノードの情報を再起的に集約してembeddingすることでグラフ構造をそのままニューラルネットに落とし込みます。
このオリジナルのGNNは近傍の情報の取り込みや計算効率に問題があるので、それを改善したGraph Convolutional Networks(GCN)[6]ここでのGCNは特にこの有名な論文の提案手法を指します。この手法は元々半教師あり学習として提案されています。がよく用いられます。GCNはGNNの派生的なもので、その名の通り畳み込みを用いる手法です[7]GCNの概念的な解説はこちら、数式の解説はこちらが分かりやすいです。。
このような手法によって、もともと特徴量で表される各ノードについてグラフの構造を加味して各ノードをベクトル化できます。[8]このGCNだとエッジの特徴量を直接取り込めていないなどの問題があります。エッジの情報を積極的に使いたい場合は、Message Passing Neural Networks (MPNN)などの手法がありますが、ここでの説明は割愛します。詳しい解説はこちらが参考になります。。
こちらのノートブック内で、GCNの畳み込み部分をPythonで実装しています。畳み込みというと難しそうですが、やってることはシンプル(行列の掛け算)です。
より詳しい説明はこちらの本をご参照いただければと思います。
注釈
| ↩1 | グラフ機械学習では、ノード分類などの下流タスクの前段として重宝されます。 |
|---|---|
| ↩2 | 行列分解の解説はこちらの記事が分かりやすいです。 |
| ↩3 | 最適化時の損失関数の工夫で、得られるembeddingの特徴を変えられる。 |
| ↩4 | 非線形な活性化関数を用いると、非線形な変換ができる。巨大なグラフには適さない。 |
| ↩5 | グラフデータを扱うニューラルネットワークについては、こちらのサーベイ発表が面白いです。 |
| ↩6 | ここでのGCNは特にこの有名な論文の提案手法を指します。この手法は元々半教師あり学習として提案されています。 |
| ↩7 | GCNの概念的な解説はこちら、数式の解説はこちらが分かりやすいです。 |
| ↩8 | このGCNだとエッジの特徴量を直接取り込めていないなどの問題があります。エッジの情報を積極的に使いたい場合は、Message Passing Neural Networks (MPNN)などの手法がありますが、ここでの説明は割愛します。詳しい解説はこちらが参考になります。 |




コメント