今回から、グラフデータに対する機械学習(グラフ機械学習)について取り上げます。
グラフ機械学習はややマニアックですが、SNS分析などに威力を発揮するツールです。
この連載では、グラフ機械学習の理論の基礎とPythonを使った実装について紹介します。
記事執筆時点で、グラフ機械学習の日本語の専門書が無いので、今回は主に以下の洋書を参考にしています[1]洋書ですが、大学の難しい専門書というよりチュートリアルのような雰囲気で読みやすいです。。
本書を読み終える頃には、グラフ理論の基本的な概念と、機械学習アプリケーションを成功させるためのアルゴリズムとテクニックをすべて習得していることでしょう。
グラフとは
ここでいうグラフとは数学的なモデルで、実体(物)同士の関係の記述に適したデータ構造になります。
グラフの例は以下の通りです。
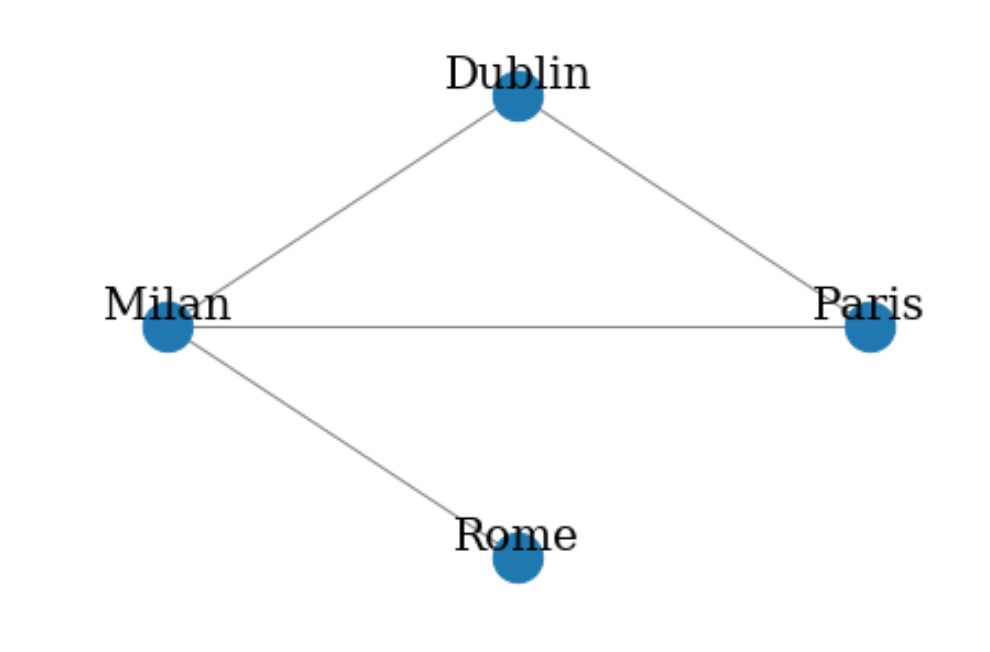
上図では都市名が線で繋がれてますが、青い丸をノード、ノードを繋いでる線をエッジと呼びます。
用語
グラフ理論でよく出てくる用語をまとめます。
- order(オーダー、位数): グラフのノードの数
(上図だとオーダーは4) - size(サイズ): グラフのエッジの数
(上図だとサイズは4) - degree(次数): 任意のノードが繋がっているエッジの数
(上図だと各ノードの次数はMailan:3, Paris:2, …)
有向グラフや無向グラフなどのグラフの種類については、ノートブック内でPythonコードと共に掲載しています。
グラフデータの表現
グラフデータ構造の表現方法として、adjacency matrix(隣接行列)があります。
隣接行列$M$はグラフ$G=(V, E)$ (V:ノード集合, E:エッジ集合)について正方行列$(|V| \times |V|)$を用いて、$\mathbf{M}_{ij}$はi→jにエッジがあるとき1, ないときは0で表します。
具体的な表現は、以下のようにグラフの種類ごとに異なります。
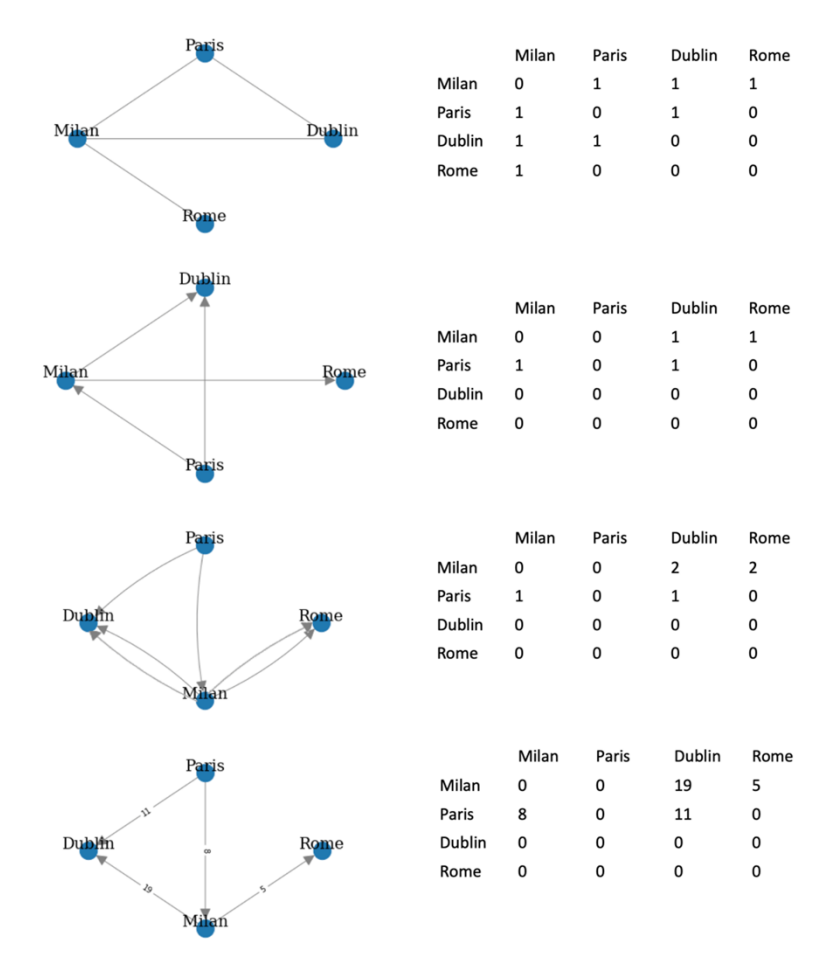
グラフのプロパティ
用語
- distance(距離): ノード$i$からノード$j$までに繋がっているエッジの数
- path(パス、道): ノード$i$からノード$j$までの(異なる)エッジの集合
- shortest path[2]こちらによると道と経路は定義が異なるようなので、shortest pathを最短経路と訳していいのか不明です。: パスのうち距離が最小のパス
- diameter(直径): 可能なすべてのshortest pathのうち、最長のshortest pathの距離
指標
グラフの特徴・性質を測定するための指標。測りたい内容に応じて、適切なメトリクスを利用する。
- Integration metrics
ノード同士がどのように相互接続されているかを定量化。
(グラフ内のグループのプレゼンスなどの扱いには不向き→Segregation metricsを使う)
- Segregation metrics
ネットワーク内の相互接続されたノードのグループ(コミュニティやモジュール、クラスターと呼ばれる)の存在を定量化。
(グラフの各ノードの重要性を扱うには不向き→Centrality metricsを使う)
- Centrality metrics
ネットワーク内の個々のノードの重要性を定量化。
指標の詳細は、ノートブック内で説明しています。
以上、グラフ理論の基礎の基礎についての説明でした。
踏み込んだ内容はノートブックでPythonソースコードとともに掲載しております。
study/graph_machine_learning/chapter1.ipynb at master · mimosom/study
Contribute to mimosom/study development by creating an account on GitHub.
より詳しい説明はこちらの本をご参照ください。
本書を読み終える頃には、グラフ理論の基本的な概念と、機械学習アプリケーションを成功させるためのアルゴリズムとテクニックをすべて習得していることでしょう。



コメント